Ray Tracing and Refraction

A few weeks ago I was following Peter Shirley’s awesome “Ray Tracing in One Week End” book. Everything went fine until I reached dielectric materials, where I started to obtain really weird pictures. From there, I had to fully re-check the ray tracer. This was both painful and beneficial, since it forced me to dig into every details of the ray tracer. The formulas for refraction are not really explained in the book. So, I decided to write a more detailed explanation in this post. Internalizing this proof actually lead me to the bug in my code, I hope that can help.

Here is a small widget that implements the formulas described in this post.

40°
Angle Out

Overview

Refraction describes how a ray behaves when crossing materials. We consider the setup depicted on Figure 1, where a ray intersects different materials (e.g., from air to water). The materials have different refractive indices \(n_{i}\) and \(n_{r}\). Let \(\vec{i}\) be the incident ray, \(\vec{r}\) the refracted ray and \(\vec{n}\) the surface normal. The question is: how can we express \(\vec{r}\) in function of \(\vec{i}\) and \(\vec{n}\) and the refractive indices?

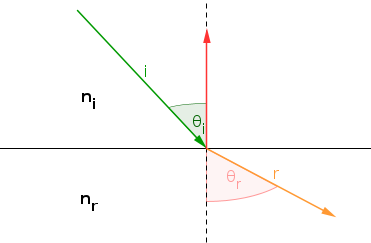
Typical Refraction Setup

Figure 1: Typical Refraction Setup

We make the following assumptions:

  • the normal vector is always oriented against the incident ray, formally \(\langle\vec{i},\,\vec{n}\rangle<0\),
  • all vectors are normalized, \(\|\vec{i}\|=\|\vec{r}\|=\|\vec{n}\|=1\).

The relation between \(\theta_{i}\) and \(\theta_{r}\) is given by Snell’s law, which states that:

\begin{equation*} n_{i}\sin\theta_{i}=n_{r}\sin\theta_{r}\label{eq:snell_law} \end{equation*}

Note that there cannot be refraction in every configuration. For refraction to be possible, we need to have:

\begin{equation*} \frac{n_{i}}{n_{r}}\sin\theta_{i}<1. \end{equation*}

When this condition is not satisfied, the ray is reflected.

The Refraction Formula

Ok, now lets see how we can compute \(\vec{r}\) from \(\vec{i}\) and \(\vec{n}\). The trick is to decompose \(\vec{r}\) as follows:

\begin{equation*} \vec{r}=\vec{r_{||}}+\vec{r_{\perp}} \end{equation*}

Where is \(\vec{r}_{||}\) is the projection of \(\vec{r}\) on \(\vec{n}\) and \(\vec{r_{\perp}}\) the projection on the orthogonal of \(\vec{n}\) in the plane generated by \(\vec{i}\) and \(\vec{n}\) . This decomposition expands as follows:

\begin{equation*} \begin{aligned} \vec{r} & = & \underbrace{\langle\vec{r},\,\vec{n}\rangle\vec{n}}_{\vec{r_{||}}}+\underbrace{(\vec{r}-\langle\vec{r},\,\vec{n}\rangle\vec{n})}_{\vec{r_{\perp}}}\label{eq:r_expansion}\end{aligned} \end{equation*}

It is easy to check that the right term is indeed orthogonal to \(\vec{n}\) (the dot product with \(\vec{n}\) is zero). Another way to express \(\vec{r}_{\perp}\) is through a cross product:

\begin{equation*} \vec{r}_{\perp}=(\vec{r}-\langle\vec{r},\,\vec{n}\rangle\vec{n})=(\vec{r}\times\vec{n})\times\vec{n}. \end{equation*}

We can expand \(\vec{i}\) in the same way we did for \(\vec{r}\).

\begin{equation*} \begin{aligned} \vec{i} & = & \underbrace{\langle\vec{i},\,\vec{n}\rangle\vec{n}}_{\vec{i_{||}}}+\underbrace{(\vec{i}-\langle\vec{i},\,\vec{n}\rangle\vec{n})}_{\vec{i_{\perp}}}\end{aligned} \end{equation*}

And we also have (keep this equality in mind, we will reuse it by the end of the proof):

\begin{equation*} \vec{i}_{\perp}=(\vec{i}-\langle\vec{i},\,\vec{n}\rangle\vec{n})=(\vec{i}\times\vec{n})\times\vec{n}\label{eq:i_perp} \end{equation*}

Now here is the trick I missed when trying to work out this proof: \(\vec{r}\) is in the plane generated by \(\vec{i}\) and \(\vec{n}\). In other words, \(\vec{i}\times\vec{n}\) and \(\vec{r}\times\vec{n}\) are colinear and as a bonus, they are linked by Snell’s law. The cross product of two vector is defined as:

\begin{equation*} \vec{i}\times\vec{n}=\|\vec{i}\|\|\vec{n}\|\sin\theta_{i}\vec{k}. \end{equation*}

Here, I introduced \(\vec{k}\) which is the orthogonal vector to the plane generated by \(\vec{i}\) and \(\vec{n}\). Similarly, for \(\vec{r}\) we have:

\begin{equation*} \vec{r}\times\vec{n}=\|\vec{r}\|\|\vec{n}\|\sin\theta_{r}\vec{k}. \end{equation*}

If we assume that \(\|\vec{i}\|=\|\vec{r}\|=1\), we can write:

\begin{equation*} \begin{aligned} \vec{r}\times\vec{n} & =\sin\theta_{r}\vec{k}\nonumber \\ & =\frac{n_{i}}{n_{r}}\sin\theta_{i}\vec{k} & \text{(Using Snell's law)}\nonumber \\ & =\frac{n_{i}}{n_{r}}\vec{i}\times\vec{n}.\end{aligned} \end{equation*}

Awesome! We are ready to expand \(\vec{r}\). Lets review the decomposition of \(\vec{r}\):

\begin{equation*} \begin{aligned} \vec{r} & = & \vec{r}_{||} + \vec{r}_{\perp}\\ & = & \langle\vec{r},\,\vec{n}\rangle\vec{n}+(\vec{r}\times\vec{n})\times\vec{n}.\end{aligned} \end{equation*}

We can now expand each term. Lets start with the left one, \(\vec{r}_{||}\):

\begin{equation*} \begin{aligned} \langle\vec{r},\,\vec{n}\rangle\vec{n} & =-\langle-\vec{r},\,\vec{n}\rangle\vec{n}\\ & =-\cos\theta_{r}\vec{n}\\ & =-\sqrt{1-\sin^{2}\theta_{r}}\vec{n}\\ & =-\sqrt{1-\left(\frac{n_{i}}{n_{\theta}}\right)^{2}\sin^{2}\theta_{i}}\vec{n}\\ & =-\sqrt{1-\left(\frac{n_{i}}{n_{\theta}}\right)^{2}\left(1-\cos^{2}\theta_{i}\right)}\vec{n}\\ & =-\sqrt{1-\left(\frac{n_{i}}{n_{\theta}}\right)^{2}\left(1-\langle-\vec{i},\,\vec{n}\rangle^{2}\right)}\vec{n}\end{aligned} \end{equation*}

In the first line, we use the basic trigonometry equation between sines and cosines, \(\cos^{2}\theta+\sin^{2}\theta=1\). In the second line, we apply Snell law. In the third line, we apply again some basic trigonometry again. The last step uses the fact that \(\cos\theta_{i}=\langle-\vec{i},\,\vec{n}\rangle\). So, we have expressed \(\vec{r_{\perp}}\) only from \(\vec{i}\) and \(\vec{n}\).

Now, it is time to expand \(\vec{r_{\perp}}\): .

\begin{equation*} \begin{aligned} (\vec{r}\times\vec{n})\times\vec{n} & =\left(\frac{n_{i}}{n_{r}}\vec{i}\times\vec{n}\right)\times\vec{n}\\ & =\frac{n_{i}}{n_{r}}\left(\vec{i}\times\vec{n}\right)\times\vec{n}\\ & =\frac{n_{i}}{n_{r}}(\vec{i}-\langle\vec{i},\,\vec{n}\rangle\vec{n})\\ & =\frac{n_{i}}{n_{r}}(\vec{i}+\langle-\vec{i},\,\vec{n}\rangle\vec{n})\end{aligned} \end{equation*}

On the first line, we rewrite the cross product, thanks to Snell's law. On the second line, we move out the scalar constant and on the last line, we use the relation shown previously.

Lets define \(\mu=\frac{n_{i}}{n_{r}}\), then \(\vec{r}\) can be written as:

\begin{equation*} \begin{aligned} \vec{r} & =\vec{r_{||}}+\vec{r}_{\perp}\\ & =-\sqrt{1-\mu^{2}\left(1-\langle-\vec{i},\,\vec{n}\rangle^{2}\right)}\vec{n}+\mu(\vec{i}+\langle-\vec{i},\,\vec{n}\rangle\vec{n})\\ & =\left(\mu\langle-\vec{i},\,\vec{n}\rangle-\sqrt{1-\mu^{2}\left(1-\langle-\vec{i},\,\vec{n}\rangle^{2}\right)}\right)\vec{n}+\mu\vec{i} \end{aligned} \end{equation*}

Back to the Code

Now, the code shown in the book should make more sense.

vec3 refract(const vec3& uv, const vec3& n, double etai_over_etat)
{
    auto cos_theta = fmin(dot(-uv, n), 1.0);
    vec3 r_out_perp =  etai_over_etat * (uv + cos_theta*n);
    vec3 r_out_parallel = -sqrt(fabs(1.0 - r_out_perp.length_squared())) * n;
    return r_out_perp + r_out_parallel;
}

Well, if you look carefully, the r_out_parallel does not match with the expression of \(\vec{r}_{||}\). The author applied Pythagoras' theorem (assuming the vector returned is a unit vector).

\begin{equation*} ||\vec{r}||^2 = ||\vec{r}_{||}||^2 + ||\vec{r}_{\perp}||^2 \end{equation*}

So,

\begin{equation*} ||\vec{r}_{||}|| = \pm \sqrt{1 - ||\vec{r}_{\perp}||^2} \end{equation*}

Since we know that \(\vec{r}_{||}\) is oriented against \(\vec{n}\), we can write:

\begin{equation*} \vec{r}_{||} = -\sqrt{1 - ||\vec{r}_{\perp}||^2}\vec{n} \end{equation*}

Pfew, while there are no fancy math involved, understanding the final refraction program was much more involved than what I initially though. Given the quantity of boring equation, I definitely understand why the author did not include them in its book!

Useful References

Here are some references that helped me debug refraction: